Why is "Differentiation" Needed in Deep Learning? (Linear Algebra, Really?)
1. Introduction: A Rational Developer’s Skepticism
When studying deep learning, you’ll encounter two mathematical giants: Linear Algebra and Calculus. As a developer, you might pause and wonder:
"The name itself is "Linear" Algebra. It’s about equations like y = ax + b… A first‑degree function, when differentiated, just leaves a constant (a). Why bother with differentiation? Just solve the equation and you’re done?"
That’s a fair point. If a deep‑learning model were truly a perfect linear function, you could find the answer (x) with a single matrix inversion.
But the real problems we tackle aren’t that simple. Today we’ll explain why we need the seemingly complex tool of differentiation and the real reason behind it, all in developer‑friendly language.
2. Differentiation = "How does tweaking this setting affect the outcome?" (Sensitivity Check)
Let’s view differentiation not as a math formula but from a system‑operations perspective.
Imagine you’re tuning a massive black‑box server with thousands of knobs.
- Goal: Reduce the server response time (Loss) as close to 0 as possible.
- Problem: You don’t know which knob to turn. The knobs are interdependent.
In this context, "doing differentiation" is a very simple act.
"If I turn knob #1 slightly to the right by 0.001 mm, does the response time improve or worsen?"
The answer to that question is the derivative (slope).
- If the derivative is positive (+) 👉 "Turning it slows things down; try the opposite direction!"
- If the derivative is negative (‑) 👉 "Nice, it speeds up; keep going that way!"
- If the derivative is 0 👉 "No change; you’re at an optimum or the knob is irrelevant."
Thus, in deep learning, differentiation isn’t about solving equations—it’s a compass that tells you which direction to adjust parameters to reduce error.
3. Why You Can’t Solve It All at Once with an Equation? (The Magic of Non‑Linearity)
Let’s revisit the earlier question: "If it’s linear, why not just solve it?"
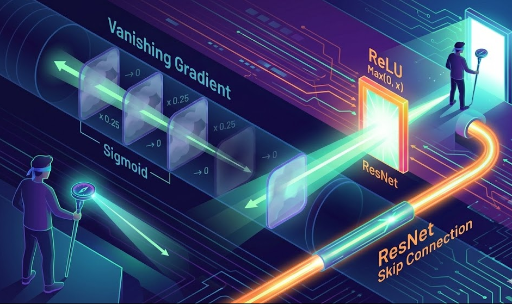
Deep learning’s power comes from sandwiching non‑linear functions like ReLU or Sigmoid between linear operations (matrix multiplications).
- Only linear: No matter how many layers you stack, it’s still just a big matrix multiplication. (y = a(b(cx)) ultimately becomes y = abcx.)
- With non‑linearity: The graph becomes a winding mountain range, not a straight line. You can’t find the optimal solution with a single equation.
So we abandon the idea of finding a closed‑form solution and instead use gradient descent—a step‑by‑step approach that walks down the mountain. That’s the essence of deep‑learning training.
4. Vector Differentiation? Just "Checking Thousands of Settings at Once"
Does "differentiating a vector" sound intimidating? In developer terms, it’s Batch Processing.
If you had only one parameter, it’s a scalar derivative. Modern models have billions of parameters (LLMs, etc.). Testing each knob individually is impossible.
Vector/matrix differentiation (Gradient) processes all those billions of questions in a single operation.
"Hey, for all 7 billion current parameters, report how the output changes if each moves a little from its current position."
That bundle of reports is the gradient vector. PyTorch, using GPUs, computes this massive report in a flash.

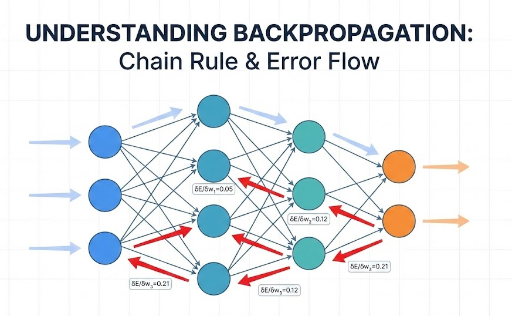
5. Wrap‑Up: The Next Step is Backpropagation
Now we know differentiation is a compass that points toward reducing error. But deep‑learning models stack dozens or hundreds of layers.
- To reduce error at the output layer, you must fix the layer just before it.
- To fix that layer, you must fix the layer before that…
This chain reaction of derivatives is efficiently computed by the famous Backpropagation algorithm.
In the next post, we’ll explore how backpropagation uses a single Chain Rule to traverse these deep networks and reveal its elegant mechanism.


There are no comments.