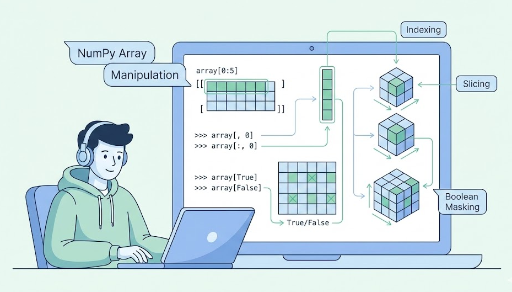
NumPy‑Indexierung & Slicing: Tensoren frei schneiden und auswählen
1. Warum ist Indexierung/Slicing so wichtig?
Beim Deep‑Learning arbeitet man häufig mit Tensoren.
- Aus einer Batch nur die ersten paar Samples auswählen
- In einem Bild nur einen bestimmten Kanal (R/G/B) nutzen
- In Sequenzdaten nur einige Zeitschritte extrahieren
- Aus Labels nur bestimmte Klassen herausfiltern
All diese Aufgaben sind letztlich „Indexierung (indexing) & Slicing“.
Da die Indexierungs‑/Slicing‑Syntax von PyTorch fast identisch mit NumPy ist, lohnt es sich, NumPy zunächst gut zu beherrschen – so wird das Schreiben von Deep‑Learning‑Code deutlich einfacher.
2. Grundlegende Indexierung: von 1‑D bis hin
2.1 Indexierung eines eindimensionalen Arrays
import numpy as np
x = np.array([10, 20, 30, 40, 50])
print(x[0]) # 10
print(x[1]) # 20
print(x[4]) # 50
- Indizes beginnen bei 0
x[i]gibt das i‑te Element
2.2 Negative Indizes
Wenn man von hinten zählen möchte, verwendet man negative Indizes.
print(x[-1]) # 50 (letztes Element)
print(x[-2]) # 40
PyTorch verhält sich genauso.
3. Grundlegendes Slicing: start:stop:step
Slicing wird in der Form x[start:stop:step] verwendet.
x = np.array([10, 20, 30, 40, 50])
print(x[1:4]) # [20 30 40], 1 ≤ i < 4
print(x[:3]) # [10 20 30], von Anfang bis 3
print(x[2:]) # [30 40 50], von 2 bis Ende
print(x[:]) # Kopie des gesamten Arrays
Mit step kann man einen Abstand festlegen.
print(x[0:5:2]) # [10 30 50], 0 bis 4 in Schritten von 2
print(x[::2]) # [10 30 50], gleich
Im Deep‑Learning ist das z. B. nützlich, wenn man Zeitschritte überspringt oder Stichproben in bestimmten Abständen auswählt.
4. Indexierung ab 2‑D: Zeilen und Spalten
Ab 2‑D wird man quasi mit Matrizen/Batchs arbeiten.
import numpy as np
X = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]]) # shape: (3, 3)
4.1 Einzelne Zeilen/Spalten
print(X[0]) # erste Zeile: [1 2 3]
print(X[1]) # zweite Zeile: [4 5 6]
print(X[0, 0]) # Zeile 1, Spalte 1: 1
print(X[1, 2]) # Zeile 2, Spalte 3: 6
X[i]→ i‑te Zeile (1‑D‑Array)X[i, j]→ Wert in Zeile i, Spalte j (Skalar)
4.2 Zeilen‑Slicing
print(X[0:2]) # Zeilen 0 und 1
# [[1 2 3]
# [4 5 6]]
print(X[1:]) # ab Zeile 1 bis Ende
# [[4 5 6]
# [7 8 9]]
Das ist ein typisches Muster, wenn man in PyTorch nur einen Teil der Batch nutzt.
4.3 Spalten‑Slicing
print(X[:, 0]) # alle Zeilen, Spalte 0 → [1 4 7]
print(X[:, 1]) # alle Zeilen, Spalte 1 → [2 5 8]
:bedeutet „alle Elemente in dieser Dimension“X[:, 0]bedeutet „alle Zeilen, Spalte 0“
Im Deep‑Learning:
- Bei einem Array
(batch_size, feature_dim)kann man mitX[:, k]einen bestimmten Feature‑Kanal extrahieren.
5. 3‑D und mehr: Batch × Kanal × Höhe × Breite
Betrachten wir Bilddaten als Beispiel.
# (batch, height, width) annehmen
images = np.random.randn(32, 28, 28) # 32 Bilder, 28×28
5.1 Ein einzelnes Sample
img0 = images[0] # erstes Bild, shape: (28, 28)
img_last = images[-1] # letztes Bild
5.2 Teil einer Batch
first_8 = images[:8] # die ersten 8, shape: (8, 28, 28)
5.3 Bild‑Crop (nur ein Teilbereich)
# mittleres 20×20‑Bereich
crop = images[:, 4:24, 4:24] # shape: (32, 20, 20)
In PyTorch sieht das ähnlich aus:
# images_torch: (32, 1, 28, 28)
center_crop = images_torch[:, :, 4:24, 4:24]
Die Indexierungs‑/Slicing‑Prinzipien sind also nahezu identisch.
6. Slicing erzeugt meist einen View
Ein wichtiger Punkt:
Das Ergebnis eines Slicings ist in der Regel ein View des Original‑Arrays. Das bedeutet, es wird nicht kopiert, sondern man sieht nur einen Teil des Originals.
x = np.array([10, 20, 30, 40, 50])
y = x[1:4] # View
print(y) # [20 30 40]
y[0] = 999
print(y) # [999 30 40]
print(x) # [ 10 999 30 40 50] ← Original geändert!
Vorteil: Speicher‑ und Zeitersparnis. Nachteil: Unabsichtliche Änderungen am Original.
Um einen echten, unabhängigen Array zu erhalten, nutzt man copy().
x = np.array([10, 20, 30, 40, 50])
y = x[1:4].copy()
y[0] = 999
print(x) # [10 20 30 40 50], Original bleibt unverändert
PyTorch hat ein ähnliches Konzept, daher ist es hilfreich, den Unterschied zwischen View und Copy zu kennen.
7. Boolesche Indexierung: Elemente nach Bedingung auswählen
Boolesche Indexierung wählt nur die Elemente, die eine Bedingung erfüllen.
import numpy as np
x = np.array([1, -2, 3, 0, -5, 6])
mask = x > 0
print(mask) # [ True False True False False True]
pos = x[mask]
print(pos) # [1 3 6]
x > 0erzeugt ein Bool‑Arrayx[mask]wählt dieTrue‑Positionen
Beispiel mit 2‑D:
X = np.array([[1, 2, 3],
[4, 5, 6],
[-1, -2, -3]])
pos = X[X > 0]
print(pos) # [1 2 3 4 5 6]
Im Deep‑Learning wird das häufig genutzt, z. B. um:
- Nur Samples mit einer bestimmten Klasse zu extrahieren
- Beim Verlustrechnen einen Masken‑Filter anzuwenden
PyTorch verhält sich analog:
import torch
x = torch.tensor([1, -2, 3, 0, -5, 6])
mask = x > 0
pos = x[mask]
8. Integer‑Array / List‑Indexierung (Fancy Indexing)
Man kann auch ein Array oder eine Liste von Ganzzahlen als Index verwenden, um mehrere Positionen gleichzeitig zu holen.
x = np.array([10, 20, 30, 40, 50])
idx = [0, 2, 4]
print(x[idx]) # [10 30 50]
Auch in 2‑D funktioniert das.
X = np.array([[1, 2],
[3, 4],
[5, 6]]) # shape: (3, 2)
rows = [0, 2]
print(X[rows])
# [[1 2]
# [5 6]]
Im Deep‑Learning kann man z. B. mit einer zufälligen Index‑Liste Batch‑Samples ziehen oder nur bestimmte Labels/Predictions sammeln.
9. Häufige Indexierungs‑Patterns zusammengefasst
Hier ein Überblick über typische Muster aus der Deep‑Learning‑Praxis:
import numpy as np
# (batch, feature)
X = np.random.randn(32, 10)
# 1) Nur die ersten 8 Samples
X_head = X[:8] # (8, 10)
# 2) Nur ein bestimmtes Feature (z. B. Spalte 3)
f3 = X[:, 3] # (32,)
# 3) Nur gerade Indizes
X_even = X[::2] # (16, 10)
# 4) Nur Samples mit Label 1
labels = np.random.randint(0, 3, size=(32,))
mask = labels == 1
X_cls1 = X[mask] # Samples mit Label 1
# 5) Zufälliges Shuffeln, dann 24 für train, 8 für val
indices = np.random.permutation(len(X))
train_idx = indices[:24]
val_idx = indices[24:]
X_train = X[train_idx]
X_val = X[val_idx]
Diese Muster gelten auch für PyTorch‑Tensoren. Im Grunde bedeutet NumPy‑Indexierung beherrschen: man kann Tensoren frei „schneiden, mischen, auswählen“.
10. Fazit
Zusammengefasst:
- Indexierung:
x[i],x[i, j], negative Indizes - Slicing:
start:stop:step,:, multidimensional (X[:, 0],X[:8],X[:, 4:8]) - Slicing erzeugt meist einen View – bei Bedarf
copy()nutzen - Boolesche Indexierung: Filter mit Bedingungen (
x[x > 0],X[labels == 1]) - Integer‑Array‑Indexierung: Mehrere Positionen gleichzeitig (
x[[0,2,4]])
Wenn man diese Techniken beherrscht, kann man mit PyTorch‑Tensoren Batch‑Slicing, Kanal‑Auswahl, Masken‑Anwendung und Sample‑Mischung viel einfacher durchführen.



Es sind keine Kommentare vorhanden.